Mahmudul FAISAL Al Ameen

Functional Style Programming Using C

Mahmudul FAISAL Al Ameen

Dec 14, 2018
32 Min read
39,489 Views

Dec 14, 2018
32 Min read
39,489 Views

C/C++

Introduction

Learning programming and learning programming language are not the same. Most of our textbooks teach us programming languages. In truth, a programming language is just a tool that we use to implement an executable program. We need resources that teach us how to solve problems using a programming language.

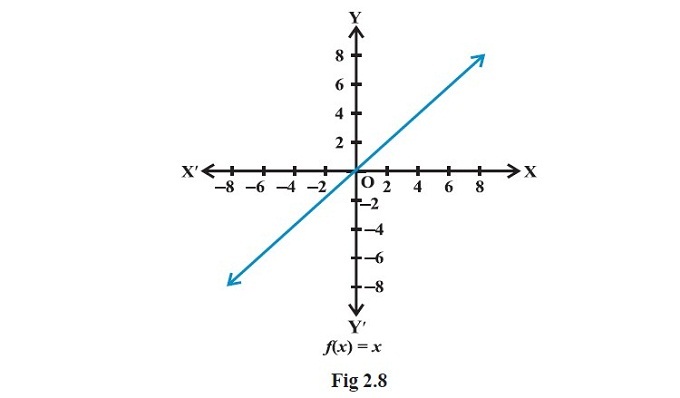
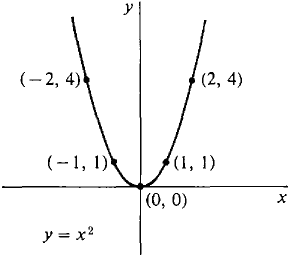
As early as elementary school, we learned what is a mathematical function and how to write it. For example, f(x)=x^2 is a simple quadratic function.

A function describes a mathematical statement. The above function maps the relationship between two sets of natural numbers as given at the right in the graph below. Often, it is impossible to show such a mapping graphically when we have a large number of discrete elements in either of the sets. Therefore, for convenience, we express a function by writing it as an inherent relation between the sets.

description

This is perhaps the simplest way to demonstrate relationships when we deal with sets of numbers (integer, natural number, real numbers, complex numbers, etc.)

We can also think of a function as a machine which has taken in inputs and produces an output by using a mechanism that maps the relationship from input to output. The sets to which the inputs and output belong are also important. A function often has a name that allows us to identify it. Typically a function is deterministic, it can produce only a single output from a unique set of inputs.

Philosophical Background

Using different mathematical strategies, we can solve problems under various domains.

One philosophical foundation of computer programming was to represent or express all kinds of mathematical problems by a single language and solve them using generalized mathematics. The result was two equivalent systems, the Turing machine and lambda calculus.

The concept of a Turing machine influenced imperative programming paradigm such as those of Assembly, C, C++, Java, Ruby, Python, and other programming languages.

On the other hand, lambda calculus influenced the birth of several functional languages such as LISP, ML, Haskell, and Erlang.

Although we can solve many more problems by using those programming languages than by using high school math, it is often easy to learn programming by solving smaller problems first. In this book (or booklet), we will learn how to solve a problem of known category. In the beginning, we will see how a simple arithmetic function can be converted into a computer program. Later, we will learn to convert more complex functions. We will also learn how to compose a function using other functions. A function can also be built using itself through recursion. We will see how they can be converted using usual pattern matching.

Rather than learning alien text, we will try to use our common sense, simple IQ and pattern matching to convert a mathematical function into a computer program. Although we will write all the code in the language C, any other language can be used instead. If we use other languages, we may need to transform the given programs to that target language. So, if we do not know any other language, it is better to stick to C.

Anyway, instead of coding (writing in a computer to execute it physically) the converted code in this book, we will try to learn the programs by jotting it down independently. Initially, most problems given here are small and easy to write on a notebook (paper) by pen or pencil. In this way, the learner becomes familiar with the relationship between theoretical formulas and the implemented programs.

Programs for Unary Arithmetic Function

We will convert some basic functions into programs in this section. First, we will see how to write programs for unary functions. Later, we will learn the same of binary and n-ary function.

Identity Function

The identity function (or a function in which output mirrors the input) looks like this:

description

Function id(x) = x can be converted into:

1int id(int x){
2	return x;
3}

Successor Function

Successor functions use the + operator to add 1 to the input and return its successor.

Operator	Name
`+`	Addition
`-`	Subtraction
`*`	Multiplication
`/`	Division
`%`	Reminder

Function suc(x) = x + 1 can be converted to:

1int suc(int x){
2	return x + 1;
3}

Twice Function

This is defined as twice(x) = 2x in arithmetic.

In C, the same function takes the form below.

1int twice(int x){
2	return 2 * x;
3}

Square Function

This function is defined as square(x) = x^2 arithmetically.

In C, it takes the form below.

1int square(int x){
2	return x * x;
3}

Here we present a pictorial representation of the above function square where the parameter x is mutiplied with itself to produce and return the result.

description

Polynomial Function

In arithmetic, the function is defined as: poly_1(x) = x^2 + 1

It can be converted into a programming function as shown below:

1int poly1(int x){
2	return x * x + 1;
3}

In arithmetic, the function is defined as: poly2(x) = x^4 + x^2 + 1

It can be converted into a programming function as shown below:

1int poly2(int x){
2	return (x * x * x * x) + (x * x) + 1;
3}

This can be simplified:

1sum_{i=1}^ni = n(n+1)/2

It can be converted into a programming function as:

1int sum(int n){
2	return n * (n + 1) / 2;
3}

Exercise

Convert the arithmetic functions into programming function:

f1(x) = x + 2$ $f2(x) = x^3$ $f3(x) = 2x^2 + 3

f4(x) = 3x^3 + 4x^2 + 7$ $_1(m) = m(m+1)(2m+1)/6

sumOfSquare_2(m) = m^3/3 + m^2/2 + m/6$ $_1(m) = (m(m+1)/2)^2

sumOfSquare_2(m) = m^4/4+m^3/2+m^2/4

(y) = y - 1

(z) = z / 2

Programs for Binary Function

function, such as ‘add’ in arithmetic can be defined as: add(x, y) = x + y

It can be converted into a programming function as:

1int add(int x, int y){
2	return x + y;
3}

function in arithmetic – addSquare(x, y) = x^2 + 2xy + y^2

It can be converted into a programming function as:

1int addSquare(int x, int y){
2	return (x * x) + (2 * x * y) + (y * y);
3}

Comparison

Now we will solve a problem of determining the larger number between two numbers. In this case, we will construct a function that takes two parameters and it will return 1 if the first parameter is larger than the second parameter and 0 otherwise. For that we will introduce a new operator >.

a > b is 1 or (True in meaning) if a is larger than b. Otherwise it is 0 (False in meaning). So, our function is – isLarger(x, y) = x > y

The corresponding program is:

Operator	Name
`>`	Greater than
`>=`	Greater than or equal to
`<`	Smaller than
`<=`	Smaller than or equal to
`==`	Equals to
`!=`	Not equals to

1int isLarger(int x, int y){
2	return x > y;
3}

Exercise

Convert the arithmetic functions into programming function:

sub(x,y) = x - y

addOfSquare(x,y) = (x times x) + (y times y)

subOfSquare(x,y) = (x times x) - (y times y)

subOfSquare_1(x,y) = (x+y)(x-y)

g(a,b) = a + ab + b

Write functions in arithmetic and programming to – multiply two numbers. calculate average of two numbers. determine if the two given numbers are equal. determine if the two given numbers are not equal.

Programs for n-Ary Function

3-ary Function

A ternary function takes three parameter. For example: avgOfThree(x, y, z) = (x + y + z) / 3

It can be converted into a programming function as:

1int avgOfThree(int x, int y, int z){
2	return (x + y + z) / 3;
3}

N-ary Function

In a n-ary function, number of parameters is n. In this example, square of distance is an useful function to compare two distances.

The squareOfDistance function: squareOfDistance(x_1, y_1, x_2, y_2) = (x_1-x_2)(x_1-x_2) + (y_1-y_2)(y_1-y_2)

Can be converted into a programming function as:

1int squareOfDistance(int x1, int y1, int x2, int y2){
2	return (x1-x2)*(x1-x2) + (y1-y2)*(y1-y2);
3}

Square of Distance

A function can be composed using other functions. It often simplifies the expression. For example, the function, squareOfDistance can be simplified if we use the function square. It is shown here:

1square(x) = x times x
2
3squareOfDistance_1(x_1,y_1,x_2,y_2) = square(x_1-x_2)+square(y_1-y_2)

Let us write it in a programming language:

1int square(int x){
2	return x * x;
3}
4int squareOfDistance1(int x1, int y1, int x2, int y2){
5	return square(x1-x2) + square(y1-y2);
6}

Here we can see that the function squareOfDistance1 is using two copies of the function square. It is very important to understand.

The Function `Poly2`

The old function was defined as Poly2(x) = x^4 + x^2 + 1.

Now we will re-define it as Poly2_1 using the function square:

1square(x) = x times x
2
3Poly2_1(x) = square(square(x)) + square(x) + 1

In C, we can write it as:

1int square(int x){
2	return x * x;
3}
4
5int poly21(int x){
6	return square(square(x)) + square(x) + 1;
7}

The Function `sumOfQube`

The old function was defined as sumOfQube_1(x) = (x(x+1)/2)^2.

Now we will re-define it as sumOfQube using the function square and sum:

1square(x) = x times x
2
3sum(x) = (square(x) + x) / 2
4
5sumOfQube(x) = square(sum(x))

In C, we can write it as:

1int square(int x){
2	return x * x;
3}
4
5int sum(int x){
6	return (square(x) + x) / 2;
7}
8
9int sumOfSquare(int x){
10	return square(sum(x));
11}

Exercise

Prove that:

x^3 = x times square(x)

x^8 = square(square(square(x)))

Simplify them by composing other functions and write programs accordingly:

qube_c(x) = x^3

toPower8(x) = x^8

toPower4(x) = x^4

Write programs for:

parabola(a,b,c,x) = ax^2 + bx + c

square_p(x) = parabola(1,0,0,x)

qube_p(x) = parabola(x,0,0,x)

Write program for toPower4_p(x) = parabola(parabola(1,0,0,x),0,0,x) and prove that toPower4_p(x) = x^4.

Condition

From this chapter, we will not write same function twice.

General Idea

In a function, we may get different result based on different conditions on the parameters. For example, the function absolute negates its parameter if it is negative so that it can be turned into positive (negative of negative is positive) to produce the result. Otherwise (when parameter is already positive), it returns back the result exactly same as the parameter. Thus, the function can be written as:

1abs(x) = begin{dcases*}
2        x & when `x geq 0`
3        -x & otherwise
4        end{dcases*}

Compute based on conditions of parameters.

The general idea of a conditional function is as follows:

1f(x) = begin{dcases*}
2        e_1 & when `1^{st}` condition satisfies
3        e_2 & when `2^{nd}` condition satisfies
4        e_3 & when `3^{rd}` condition satisfies
5        dots & dots
6        e_n & otherwise
7        end{dcases*}

The corresponding code is:

1int f(int x){
2	if( 1st condition )
3		return e1;
4	else if( 2nd condition )
5		return e2;
6	else if( 3rd condition )
7		return e2;
8	...
9		...
10	else
11		return en;
12}

Now we will present some functions those use conditions.

if …else…

Absolute

1abs(x) = begin{dcases*}
2        x & when `x geq 0`
3        -x & otherwise
4        end{dcases*}

It's code:

1int abs(int x){
2	if( x >= 0 )
3		return x;
4	else
5		return -x;
6}

Filter

1filter_{LT}(x,y) = begin{dcases*}
2        x & when `x geq y`
3        0 & otherwise
4        end{dcases*}

Its code:

1int filterLT(int x, int y){
2	if( x >= y )
3		return x;
4	else
5		return 0;
6}

if …else …+ Composition

By composing functions, we can construct many familiar functions. Although they are not always more efficient, for obvious reason, we will do it.

Here the function abs is rewritten as:

1switcher(a,b,c,d) = begin{dcases*}
2        c & when `a geq b`
3        d & otherwise
4        end{dcases*}
5
6abs_1(x) = switcher(x, 0, x, -x)

In C:

1int switcher(int a,int b,int c,int d){
2	if(a >= b)
3		return c;
4	else
5		return d;
6}
7int abs1(int x){
8	switcher(x, 0, x, -x);
9}

Tuition Fee Calculator

Lets think a problem.

Calculate your total tuition fee due based on the condition that if your due of previous semester tuition fee is more that 1000 currency, your total fee to pay this semester will be double of previous due plus the fee of current semester. We can write a function to describe it mathematically.

1tftp(p, c)=begin{dcases*}
2        2 times p + c & when `p > 1000`
3        p + c & otherwise
4        end{dcases*}

If we use the function switcher, we can rewrite it as:

1hbox{em tftp}_1(p, c) =
2    switcher(p, 1001, 2 times p, p) + c

or,

1hbox{em tftp}_2(p, c) =
2    switcher(p, 1001, p, 0) + p + c

In programming, the functions are:

1int switcher(int a,int b,int c,int d){
2	if(a >= b)
3		return c;
4	else
5		return d;
6}
7int tftp1(int p, int c){
8	return switcher(p, 1001, 2 * p, p) + c;
9}
10int tftp2(int p, int c){
11	return switcher(p, 1001, p, 0) + p + c;
12}

Well, the parameters p and c does not mean anything. So, often it misleads us if we use meaningless names. It is also important to be able to read them easily. We can take different approaches to avoid confusions and increase readibility. They are shown as the function tftp2 is rewritten as:

1/*
2tftp: tuition fee to pay
3*/
4int tftp2(int p, int c){
5	/*
6	p: previous month's due
7	c: current month's fee
8	*/
9	return switcher(p, 1001, p, 0) + p + c;
10}

Or, in the best style:

1int tftp2(int previousDue, int currentFee){
2	return switcher(previousDue, 1000,
3					previousDue, 0)  
4					+ previousDue
5					+ currentFee;
6}

Or, in a good style:

1int tftp2(int preDue, int curFee){
2	return switcher(preDue, 1001, preDue, 0)
3			+ preDue + curFee;
4}

Or, we can write a word to keep it small and yet understandable:

1int tftp2(int due, int fee){
2	return switcher(due,1001,due,0)+due+fee;
3}

if …else if …else …

Grade Letter (in numeric)

In this example, we will solve a problem of determining the grade letter based on the total mark in an examination. The grade distribution is given at the right side.

Range Grade	letter	In numeric
90-100	A	1
80-89	B	2
70-79	C	3
60-69	D	4
40-59	E	5
0-39, <0, >100	F	6

The function that solves the problem is:

1getGrade(mark) = begin{dcases*}
2        1 & when `mark geq 90` and `mark leq 100`
3        2 & else when `mark geq 80`
4        3 & else when `mark geq 70`
5        4 & else when `mark geq 60`
6        5 & else when `mark geq 40`
7        6 & otherwise
8        end{dcases*}

Hence, the code for the above function is:

1int getGrade(int mark){
2	if( mark >= 90 && mark <= 100)
3		return 1;
4	else if( mark >= 80 )
5		return 2;
6	else if( mark >= 70 )
7		return 3;
8	else if( mark >= 60 )
9		return 4;
10	else if( mark >= 40 )
11		return 5;
12	else
13		return 6;
14}

In the above example, the function gives us a numeric value that in our mind represents a grade. But it is often necessary to give user a direct result instead of a numerical representation. If the function can generate result with letter grades directly, it will be definitely more understandable as shown here:

1getGradeLetter(mark) = begin{dcases*}
2        hbox{'A'} & when `mark geq 90` and `mark leq 100`
3        hbox{'B'} & else when `mark geq 80`
4        hbox{'C'} & else when `mark geq 70`
5        hbox{'D'} & else when `mark geq 60`
6        hbox{'E'} & else when `mark geq 40`
7        hbox{'F'} & otherwise
8        end{dcases*}

Since the letter grades are actually letters or characters, we need to change the data type of the function to ‘char’. ‘char’ type corresponds to the characters. In other words, ‘char’ is the set of all characters or visible symbols a computer can show.

Type	Nature of Data
int	integer
long	large integer
long long	very large integer
float	real number
double	large real number
char	character

The code for the above function is:

1char getGradeLetter(int mark){
2	if( mark >= 90 && mark <= 100)
3		return 'A';
4	else if( mark >= 80 )
5		return 'B';
6	else if( mark >= 70 )
7		return 'C';
8	else if( mark >= 60 )
9		return 'D';
10	else if( mark >= 40 )
11		return 'E';
12	else
13		return 'F';
14}

switch …case …

Item Price

In this example, we will solve a problem of getting prices of different items in an restaurant. We will determine an item by its item no. The prices for different item numbers are given at the right.

Item Item	No.	Price
Fish Curry	1	60.00
Fish Fry	2	80.00
Beef Curry	3	100.50
Beef Vuna	4	130.75
Chicken	5	85.00
Rice	6	15.25
Water	7	20.00
Cold Drinks	8	15.00

The function that solves the problem is:

1{hbox{em getPrice}}({hbox{em item}}) = begin{dcases*}
2        60.00 & when {em item} `= 1`
3        80.00 & when {em item} `= 2`
4        100.50 & when {em item} `= 3`
5        130.75 & when {em item} `= 4`
6        85.00 & when {em item} `= 5`
7        15.25 & when {em item} `= 6`
8        20.00 & when {em item} `= 7`
9        15.00 & when {em item} `= 8`
10        0 & otherwise
11        end{dcases*}

Hence, the code for the above function is:

1float getPrice(int item){
2	switch( item ){
3		case 1:
4			return 60.00;
5		case 2:
6			return 80.00;
7		case 3:
8			return 100.50;
9		case 4:
10			return 130.25;
11		case 5:
12			return 85.00;
13		case 6:
14			return 15.25;
15		case 7:
16			return 20.00;
17		case 8:
18			return 15.00;
19		default:
20			return 0;
21	}
22}

Type	Range
int/long	`-2^{31}` to `2^{31} - 1`
long long	`-2^{63}` to `2^{63} - 1`
float	`1.2E-38` to `3.4E+38`
double	`2.3E-308` to `1.7E+308`
long double	`3.4E-4932` to `1.1E+4932`
char	`-128` to `127`

Note: 2^{31}=2,147,483,648 and 2^{63}=9,223,372,036,854,775,808

For a realistic approach, we can add a simple function with it that calculates total price of an item for a quantity:

1calcTotalPrice(item, quantity) = quantity times getPrice(item)

The code:

1float calcTotalPrice(int item, int quantity){
2	return quantity * getPrice( item );
3}

Recursions

Easy tricks to repeat

Recursion is a technique that enhances capabilities of programs very much. For example, if we want to write an exponential function exp(x,k)=x^k, we understand that x have to be multiplied to itself k times. We can understand x^k operation from our childhood mathematics. But unfortunately C programming language does not have operator for exponential operation. We can also understand k times and we can repeat this multiplication by counting 1 to k.

But how to write the function using multiplication only? We can write exp(x,k)=x times x times dots times x (k times). If we knew k is 2, the expression becomes exp(x,2) = x times x, if it is 3, the expression is exp(x, 3) = x times x times x and so on. But when k is unknown, then it is difficult to write in very clear way. Most importantly, C programming does not support any expression like ‘x times x times dots times x (k times)’.

Intuition of Recursive definition

We use recursion to express such functions or programs. Recursion is a special kinds of composition where the definable function itself is composed with something else to define itself. It may heard weird or twisted at the first time. We will see some analogous definition in our society to understand its power.

But just imagine a simple definition of human (according to Quran and Bible):

‘Adam and Eve were human and any living mammal that borns from another human is a > human’.

This definition certainly covers all the humans. Here human is defined from the definition of another human and it is called recursion or induction. In recursive (or inductive) defintion, there must be at least one base point for example ‘Adam was human and Eve was human’.

Let us take another example, the definition of natural numbers. Suppose we have all kinds of numbers on our knowledge including real numbers, complex numbers, etc.. We need to define natural number. Here is the plain definition - 0 is a natural number and n+1 is a natural number if n is a natural number. We can use it to write a function to know whether a number is natural

1{hbox{em isNatural}}(x)=begin{dcases*}
2        {hbox{em true}}& when `x=0`
3        {hbox{em false}}& when `x<0`
4        {hbox{em isNatural}}(x-1) & otherwise
5        end{dcases*}

Similarly we can write another function to distinguish an animal as human:

1{hbox{em isHuman}}(x)=begin{dcases*}
2        {hbox{em true}}& when `x=` {em Adam}
3        {hbox{em true}}& when `x=` {em Eve}
4        {hbox{em false}}& when `x=` {em Amoeba}
5        {hbox{em isHuman}}({hbox{em mother of }}x) & otherwise
6        end{dcases*}

It says, x is a human if x is Adam or Eve. x is not human if x is Amiba. Besides x is also human if and only if mother of x is also human. Well, in the real process, to justify an animal as human, we need to know the total family tree from Adam and Eve which is very unrealistic. But the definition itself is very intuitive.

In mathematics and computer science, this recursive style of definition often expresses a fact in a very simple and intuitive way, which helps to formalize an algorithm or program in very effective way.

To create a recursive definition of a function, we need to forget how it really works. We simply need to know if the definition is correct mathematically.

For an easy construction of the definition, here we would like to present a tips. We have to remember that the function has one (or more) driving parameter(s).

Base cases part

Need to determine the value of the function for the base case(s) of the driving parameter(s). For example, exp(n,x)=1 when x=0.

Recursion part

The function itself will be appeared with smaller (typically 1 step) value or size of the driving parameter(s). For example, exp(x-1). This is called induction hypothesis (HI).

The induction hypothesis often needs to be computed with something else to be equal to the original definition. For example, exp(x)=x times exp(x-1).

Other parameters remain the same in recursion call inside the body.

If we follow the above steps, it will help us to construct recursive definition. We will explore some examples soon. In some examples, we will see how the function is constructed from the above tips. We will also see whether definition is correct.

Exponential

We will define exp(x,k). Here x is the base and k is the power. So, k is the driving parameter. Now we know the base case when k=0 - exp(x,0) = 1. Next, we will have to construct the recursion part. First, we know that the expression exp(x,k-1) exists in this part because the 1 step smaller value of k is k-1. x will remain same. Now it is necessary to multiply it to x to be equal to exp(x,k). Therefore, the full expression becomes exp(x,k) = x times exp(x,k-1). Now together the function is looks like:

1exp(x,k) =
2        1, when `k=0`
3        x times exp(x,k-1), otherwise

Obviously, the code for the above function is:

1int exp(int x, int k){
2	if( k == 0 )
3		return 1;
4	else
5		return x * exp( x, k-1 );
6}

Proof of correctness

Let us see whether the above function, exp(x,k) is really x^k. We can prove it by using induction on k.

Case 1. k=0.

`exp(x,0) = 1`	…(1) from the function
`x^0=1`	…(2) naturally
`herefore exp(x,0) = x^0`	from (1) and (2)

Case 2. k eq 0.

We want to prove that exp(x,k)=x^k. So, naturally exp(x,k-1) supposed to be x^{k-1}. We will take this as the induction hypothesis.

`exp(x,k-1) = x^{k-1}`	…(1) by induction hypothesis
so, `x times x^{k-1} = x^{k-1+1}`	we know from arithmatic
so, `x times x^{k-1} = x^k`	`k-1+1=k`
so, `x times exp(x,k-1) = x^k`	from (1)
`herefore exp(x,k) = x^k`	from the function

Factorial

Factorial is another arithmetic function that is informally, x! = x times (x-1) times ... times 1 . We can define it recursively. First, it has the only parameter, x. We know that x can be at least 0 and factorial(0)=1. This is our base part. Now in the recursion part it must contain factorial(x-1). Finally, we can multiply it with x to make it equal to factorial(x). See the proof later for a better understanding.

Now our function looks like:

1factorial(x)=
2        1 , when `x=0`
3        x times factorial(x-1), otherwise

Obviously, the code for the above function is:

1int factorial(int x){
2	if( x == 0 )
3		return 1;
4	else
5		return x * factorial( x - 1 );
6}

Proof of correctness

Let us see whether the above function, factorial(x) is really x!. We can prove it by using induction on x.

Case 1. x=0.

factorial(0) = 1 by definition, 0! = 1

Case 2. x eq 0.

We want to prove that factorial(x)=x!. So, naturally factorial(x-1) supposed to be (x-1)!. We will take this as the induction hypothesis.

`factorial(x-1) = (x-1)!`	…(1) by induction hypothesis
`(x-1)! = (x-1) times (x-2) times ... times 1`	expanded form
so, `x times (x-1)! = x times (x-1) times (x-2) times ldots imes 1`	multiplying both side by `x`
so, `x times factorial(x-1) = x!`	from (1)
`herefore factorial(x) = x!`	from the function

Fibonacci

Now our function looks like:

1{hbox{em fibonacci}}(x)=begin{dcases*}
2        0 & when `x=0`
3        1 & when `x=1`
4        {hbox{em fibonacci}}(x-1) + {hbox{em fibonacci}}(x-2) & otherwise
5        end{dcases*}

Obviously, the code for the above function is:

1int fibonacci(int x){
2	if( x == 0 )
3		return 0;
4	else if( x == 1 )
5		return 1;
6	else
7		return fibonacci( x - 1 ) +
8				fibonacci( x - 2 );
9}

Addition

1{hbox{em add}}(x,y)=begin{dcases*}
2        x & when `y=0`
3        suc({hbox{em add}}(x,y-1)) & otherwise
4        end{dcases*}

Obviously, the code for the above function is:

1int suc(int x){
2	return x + 1;
3}
4
5int add(int x, int y){
6	if( y == 0 )
7		return x;
8	else
9		return suc( factorial( x - 1 ) );
10}

Write a recursive function to represent multiplication of two numbers by using only addition. Write a recursive function to represent integer division of two numbers by using only subtraction.

Series

1sum_{i=1}^ni^4 = 1^4 + 2^4 + ldots + n^4

Can be rewritten as:

1{hbox{em sumOfQuad}}(n)=begin{dcases*}
2        1 & when `n=1`
3        {hbox{em exp}}(n,4) + {hbox{em sumOfQuad}}(n-1) & otherwise
4        end{dcases*}

In C:

1int sumOfQuad(int n){
2	if( n == 0 )
3		return 0;
4	else
5		return exp( n , 4 ) +
6				sumOfQuad( n - 1 );
7}

A Similar Series

A similar, in fact, more generalized series is:

1sum_{i=1}^ni^k = 1^k + 2^k + ldots + n^k

It can be rewritten as:

1{hbox{em sumOfPow}}(n,k)=begin{dcases*}
2        1 & when `n=1`\n        {hbox{em exp}}(n,k) + {hbox{em sumOfPow}}(n-1,k) & otherwise
3        end{dcases*}

It is converted into the program:

1int sumOfPow(int n, int k){
2	if( n == 0 )
3		return 0;
4	else
5		return exp( n, k ) +
6				sumOfPow( n - 1, k );
7}

A Product Series

A general product series can be rewritten as:

1prod_{i=1}^ni^k = 1^k times 2^k times ldots times n^k

See how we can get a product series from the previous series by only changing the base case result and by replacing + by times in the recursion part. Obviously, we should change the name of the function.

1{hbox{em prodOfPow}}(n,k)=begin{dcases*}
2        1 & when `n=1`
3        {hbox{em exp}}(n,k) times {hbox{em prodOfPow}}(n-1,k) & otherwise
4        end{dcases*}

Here is the code:

1int prodOfPow(int n, int k){
2	if( n == 0 )
3		return 1;
4	else
5		return exp( n, k ) *
6			prodOfPow( n - 1, k );
7}

Natural Square Root

In this example, we will calculate the natural square root of a number n. A natural square root is a natural number that is an integer and also positive. We will examine a very easy function to do that. In this function, 0 will first be tested if it is the square root of n. If the square root of n is not a natural number, the smallest larger value (sqrt{n}+1) will be accepted as an approximation. For each test fails, the next natural number will be tested similarly.

The logic behind the condition square(k) >= n is that sqrt{n} = k if and only if k^2 = n and sqrt n+1 = k+1 and then (k+1)^2 > n. Since the value of k is increasing from 0 one by one, either sqrt n of sqrt n+1 will be accepted as the natural square root of n.

1int square(int x){
2	return x*x;
3}
4int squareRootNatTest(int n, int k){
5	if( square(k) >= n )
6		return k;
7	else
8		return squareRootNatTest(n, k+1);
9}
10int squareRootNat(int n){
11	return squareRootNatTest(n, 0);
12}

Can you explain how the code below determines a number as a prime?

1int doesDivides(int x, int y){
2	return (x % y) == 0;
3}
4int primeTest(int i, int n){
5	if( i == n )
6		return 1;
7	else if( doesDivides(n, i) )
8		return 0;
9	else
10		return primeTest(i+1, n);
11}
12int isPrime(int n){
13	return primeTest(2, n);
14}

Real Life Example

Robot Move

Problem: Suppose we have a two-dimensional grid of N columns and M rows. We name a cell of it in terms of its vertical and horizontal index (x,y). We have a robot that can move either to one cell left or one cell below. It cannot cross the border of the grid indeed. Let’s place the robot at any cell in the grid and our current challenge is to know the number of ways it can reach to the bottom-left most corner, cell (0,0).

Solution: Lets imagine a grid of N=9 columns and M=5 rows where the robot is placed at the cell (6,3). The goal of its move is to reach the cell (0,0). It can move only downward or left.

If the robot is placed in the cell (0,0), it needs 0 move to reach the goal and hence trivially there is only one way to reach the goal. From all the cells in the left-most column ((0,1), (0,2), ldots), the robot can move only downward. So, from each of these positions (where x is 0), the robot has only one way to reach the goal. Similarly, from all the cells at bottom-most row (where y is 0), it has only one way to reach the goal. From any other cell, the path to reach the goal depends on its left and below adjacent cells. So, the number of possible ways to reach the goal can be determined by adding that of those two cells. So, our function is as follows:

1{hbox{em ways}}(x,y)=begin{dcases*}
2        1 & when `x=0` or `y=0`
3        ways(x-1,y)+ways(x,y-1) & otherwise
4        end{dcases*}

Now we can write our function in C very easily:

Operator	Name
`!`	Not
`\|\|`	Or (Logical)
`&&`	And (Logical)

1int ways(int x, int y){
2	if( x == 0 || y == 0 )
3		return 1;
4	else
5		return ways( x-1, y ) + ways( x, y-1 );
6}

LEARN MORE

Functional Style Programming Using C

Mahmudul FAISAL Al Ameen

Introduction

Philosophical Background

Programs for Unary Arithmetic Function

Identity Function

Successor Function

Twice Function

Square Function

Polynomial Function

Exercise

Programs for Binary Function

Comparison

Exercise

Programs for n-Ary Function

3-ary Function

N-ary Function

Square of Distance

The Function Poly2

The Function sumOfQube

Exercise

Condition

General Idea

if …else…

Absolute

Filter

if …else …+ Composition

Tuition Fee Calculator

if …else if …else …

Grade Letter (in numeric)

switch …case …

Item Price

Recursions

Easy tricks to repeat

**Intuition of Recursive definition**

Exponential

Factorial

Fibonacci

Addition

Series

A Similar Series

A Product Series

Natural Square Root

Real Life Example

Robot Move

The Function `Poly2`

The Function `sumOfQube`

Intuition of Recursive definition