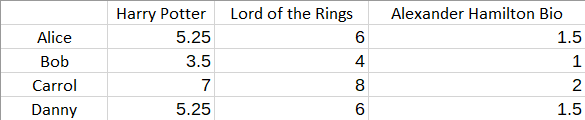Building a Recommendation Engine with TensorFlow
Aug 19, 2020 • 10 Minute Read
Introduction
Knowing how to build a recommendation engine is an important milestone in a data scientist's education. After all, recommendation engines power the hugely useful and profitable recommendation functionality of the e-commerce marketplace. Indeed, odds are you and your family have encountered something like the “Shopping for a new laptop? Here’s what people like you have bought in the past” scenario and benefited greatly.
Now, whether you are planning to join an e-commerce business as a data scientist or studying towards a Master's degree in data science, knowing how to build a recommendation engine will open doors for you and certainly be something you end up doing. To help you onboard as quickly as possible, then, this guide is going to introduce you to some of the most useful concepts you can learn to quickly construct a recommendation engine using TensorFlow.
Background
The main principle behind recommendation engines is collaborative filtering, or using knowledge from several users (“collaborators”) to make automatic predictions (“filters”). Examples of this abound, but the best known are certainly Netflix and Amazon. With Netflix, your past viewing history and reviews are used to offer you movie recommendations. Behind the scenes, techniques from collaborative filtering utilize the substantial history of other watchers’ histories and reviews to offer you the best recommendations possible. Similarly, Amazon utilizes other customers’ historical data to offer you handy product recommendations.
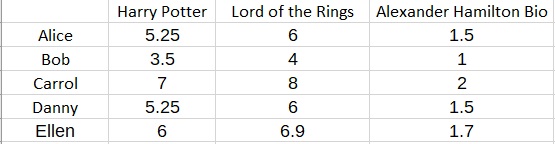
The bread-and-butter technique for collaborative filtering is called matrix factorization. This technique is famous for winning the well known “Netflix Prize” a few years back. The idea behind the technique is that there are several “latent”, or hidden, variables that are responsible for users’ ratings. For example, perhaps a user has rated books like “Harry Potter” and “Lord of the Rings” highly but the biography of Alexander Hamilton poorly. A latent variable that would explain this observation is that the highly rated books are part of the fantasy category and the user values fantasy books. Thus, we may have a latent fantasy variable.
Mathematically, the matrix of all ratings R is represented as a product of two matrices P and Q, whose inner dimensions represent the latent variables. The matrix P is the Users matrix which shows how each user rates the latent variables, and the matrix Q is the Books or Products matrix, which shows the degree to which each book or product corresponds to each latent variable.
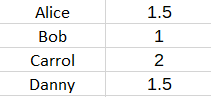
For example, suppose that there is only the fantasy latent variable. Then the P Users matrix might look like so :
This describes how much each user enjoys fantasy. The Q Books matrix might look like this:
This matrix describes the extent to which each book falls under the genre of fantasy. The product R will determine the ratings, and in this case, it is:
For us, the goal is to start with R and then compute the latent features and the matrices P and Q. Note that if some of the entries of the matrix R are missing, solving this problem can become a difficult optimization problem.
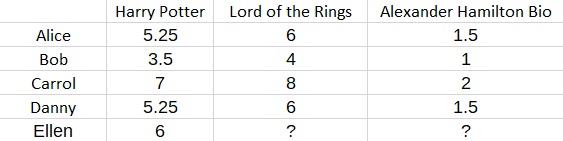
When it comes to making predictions, let’s say that you would like to predict the preferences of a new user named Ellen. Suppose additionally that we know that Ellen gave Harry Potter a score of 6.
Then we know that Ellen’s fantasy feature F must satisfy
X
=
so that
3.5F = 6
and therefore
F = 1.7
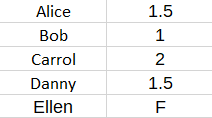
Consequently, we can fill in the rest of the matrix to obtain a prediction for Ellen:
More generally, we might have several ratings or observations for a new user (i.e., an “out-of-sample” user), such as Ellen. This user’s ratings might not fit perfectly with the matrix factorization model. But that is normal and expected. Consequently, what you should do is look for the best fitting prediction via Ordinary Least Squares.
Implementation: Training
The code for this and the following sections can be found at https://github.com/emmanueltsukerman/build-a-recommendation-engine-with-tensorflow.git
Suppose you are given a collection of ratings.
import numpy as np
ratings = np.array(
[
[3.0, 3.0, 2.0, 3.0, 3.0, 3.0],
[4.0, 1.0, 1.0, 4.0, 5.0, 3.0],
[1.0, 2.0, 2.0, 1.0, 1.0, 2.0],
[3.0, 2.0, 1.0, 3.0, 4.0, 3.0],
[1.0, 5.0, 3.0, 1.0, 1.0, 3.0],
[2.0, 5.0, 3.0, 2.0, 3.0, 4.0],
[2.0, 2.0, 1.0, 2.0, 2.0, 2.0],
[1.0, 4.0, 3.0, 1.0, 2.0, 3.0],
]
)
Load TensorFlow and specify the number of latent variables K.
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
K = 2
R = ratings
Next, configure the TensorFlow computation. Create the P and Q matrices, their product, and set the loss to be the squared error between the product of the P and Q matrices and your ratings matrix.
N = len(ratings)
M = len(ratings[0])
P = np.random.rand(N, K)
Q = np.random.rand(M, K)
ratings = tf.placeholder(tf.float32, name="ratings")
P_matrix = tf.Variable(P, dtype=tf.float32)
Q_matrix = tf.Variable(Q, dtype=tf.float32)
P_times_Q = tf.matmul(P_matrix, Q_matrix, transpose_b=True)
squared_error = tf.square(P_times_Q - ratings)
loss = tf.reduce_sum(squared_error)
Select the optimizer, in this case, gradient descent.
optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(loss)
Finally, train the model to calculate the P and Q matrices.
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
for i in range(5000):
sess.run(train, {ratings: R})
Examine the resulting matrices.
final_P_times_Q = np.around(sess.run(P_times_Q), 3)
print(final_P_times_Q)
print()
final_P_matrix = np.around(sess.run(P_matrix), 3)
print(final_P_matrix)
print()
final_Q_matrix = np.transpose(np.around(sess.run(Q_matrix), 3))
print(final_Q_matrix)
print()
[[2.721 2.93 1.932 2.721 3.375 3.185] [4.056 1.135 0.787 4.056 4.902 3.014] [0.93 2.376 1.55 0.93 1.208 1.826] [3.136 1.898 1.269 3.136 3.83 2.877] [0.846 4.844 3.146 0.846 1.206 3.099] [2.157 4.917 3.211 2.157 2.778 3.916] [1.826 1.825 1.205 1.826 2.258 2.061] [1.226 4.198 2.733 1.226 1.635 2.979]]
[[1.422 0.955] [2.364 0.085] [0.382 0.895] [1.75 0.488] [0.146 1.924] [0.931 1.83 ] [0.965 0.582] [0.424 1.621]]
[[1.705 0.39 0.275 1.705 2.057 1.22 ] [0.311 2.488 1.615 0.311 0.471 1.519]]
As you can see, the product of P and Q is a very close approximation of the original ratings. A better approximation may be possible by increasing K at the cost of a higher likelihood of overfitting.
Implementation: Prediction
Suppose that a new user has been observed with the following ratings .
new_user_indices = [1, 2, 4, 5]
new_user_ratings = [2, 2, 1, 2]
In other words, the user has given the 2nd, 3rd, 5th, and 6th products the ratings 2, 2, 1, and 2, respectively. You will now predict the remaining ratings of this user.
To do so, you will implement an Ordinary Least Squares fit for a new row of P, which through multiplication with Q will result in the matrix R having a new row corresponding to that of the new user.
new_user_P_row_initial = np.random.rand(1, K)
new_user_P_row = tf.Variable(new_user_P_row_initial, dtype=tf.float32)
new_user_P_row_times_Q = tf.matmul(new_user_P_row, final_Q_matrix)
res = tf.gather(new_user_P_row_times_Q, new_user_indices, axis=1)
squared_error = tf.square(new_user_ratings - res)
loss = tf.reduce_sum(squared_error)
optimizer = tf.train.GradientDescentOptimizer(0.01)
predict = optimizer.minimize(loss)
Run the computation.
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
for i in range(50000):
sess.run(predict)
Finally, print out the results of the computation, and you will get the new row corresponding to the new user.
final_new_user_P_row_times_Q = np.around(sess.run(new_user_P_row_times_Q), 3)
print(np.round(final_new_user_P_row_times_Q))
[[1. 2. 2. 1. 1. 2.]]
Awesome! You have successfully predicted a new user’s ratings using the history of prior ratings you had and the technique of matrix factorization.
Conclusion
You now have a basic grasp of how to create a prototype recommendation engine using matrix factorization in TensorFlow. This is a big deal. You can take this even further by learning other matrix factorization techniques such as Funk MF, SVD++, Asymmetric SVD, Hybrid MF, and Deep-Learning MF or k-Nearest Neighbours approaches.
Another great step is to try to implement a full recommendation system pipeline, as taught in this Pluralsight course.
Happy learning.
Advance your tech skills today
Access courses on AI, cloud, data, security, and more—all led by industry experts.