Applying the Mathematical MASS Model with R

What you'll learn

Before machine learning and Python made statistics a subject of MASS popular appeal, an entire generation of applied statisticians learned their craft from the famous textbook named “Modern Applied Statistics with S” by Venables and Ripley. The “S” referred to in the book’s title is the precursor of the R statistical software, which is so popular and effective for statistical analysis. The influence of this seminal work is so strong, that R actually contains a package named MASS, an acronym for the book’s title.

In this course, Applying the Mathematical MASS Model with R, you will gain the ability to use the datasets, predictive models, and specialized functions available in the MASS package in R. 

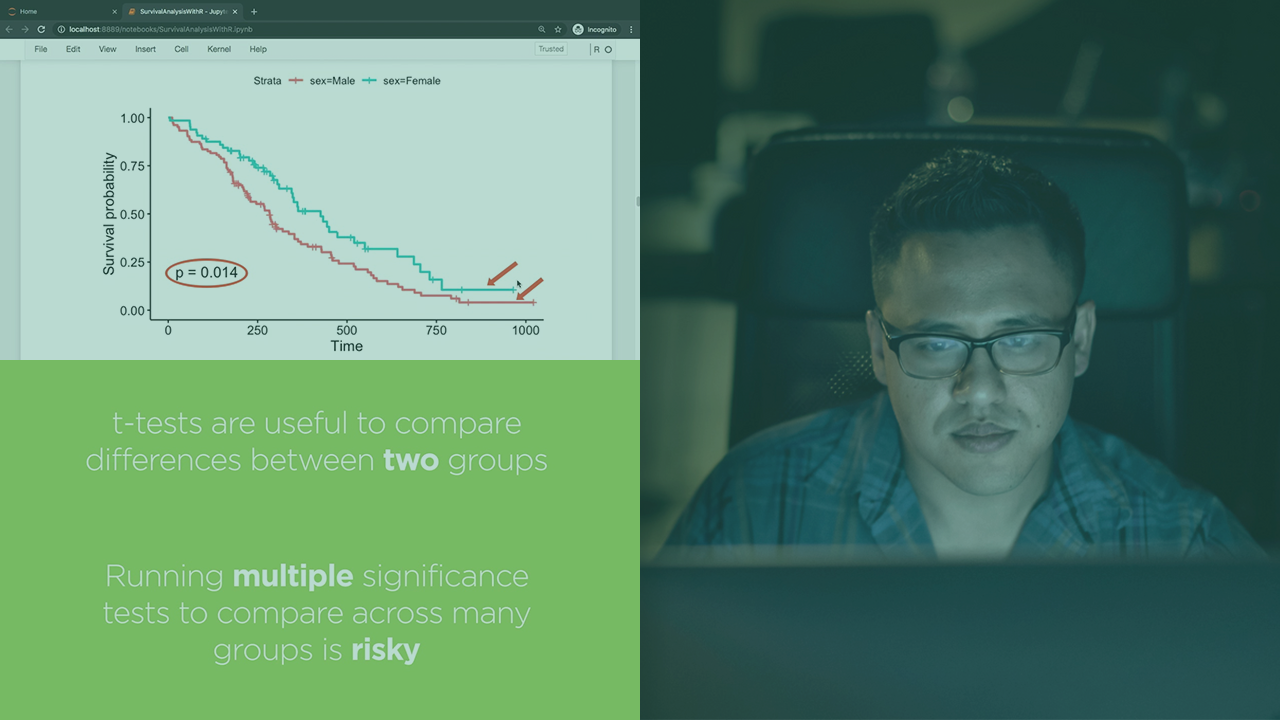
First, you will learn how the classic t-test can be used in a variety of common scenarios around estimating means and also learn about using ANOVA, a powerful statistical technique used to measure statistical properties across different categories of data. This exploration will involve variants of the t-test such as one-sample and two-sample t-tests, as well as one-way ANOVA, which is used to compare means of a target variable across different groups, based on the value of a single categorical variable.

Next, you will discover about three powerful techniques in data analysis, namely linear discriminant analysis (LDA), quadratic discriminant analysis (QDA), and robust regression. LDA and QDA are classification techniques that both seek to re-orient the original data using new, optimized axes such that points belonging to different classes lie as far apart as possible. QDA is preferable to LDA when the x-variables that correspond to different y-variable values have differing covariances. MASS includes support for three powerful robust regression techniques, Huber, Bisquare, and Hampel; each of these is a useful way to fit a regression model even when data is heavily contaminated by outliers.

Finally, you will explore how to model complex systems using multi-state models, which represent the result of a stochastic process as a succession of states. You will understand the differences - and similarities - between transition probabilities and transition intensities, and then apply all of that knowledge to a special class of multi-state models: survival models. Such models find wide applications in medical domains such as modeling outcomes of different treatment regimens, and you will learn how to do so, and also how to model hazard rates and survival probabilities. When you’re finished with this course, you will have the skills and knowledge of several specialized statistical techniques that are featured in the MASS library in R.

Table of contents